Question

C(x)=2x^3+3x^2-1 find rational zeros

Answer 1

1/2

Explanation:

The Rational Root Theorem says that any rational root has

1. a numerator that is a factor of the constant term

2. a denominator that is a factor of the leading coefficient (that's attached to the highest-power term)

Numerator:
`\pm 1`

Denominator:
`\pm 2`

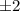
That means there are only two possible rational roots:
`\pm (1)/(2)`

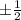
Try them both by plugging them into the polynomial.

`2\left((1)/(2)\right)^3 + 3\left((1)/(2)\right)^2 -1= (1)/(4)+(3)/(4)-1 =0`

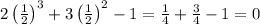
Aha! The negative one-half value does not produce 0