Question

Question #6
Show steps
Correct answer is A

Answer 1

We'll first need to determine what the composite function f(g(x)) is equal to.

Start with the outer function f(x). Then replace every copy of x with g(x). Afterward, plug in g(x) = 3x-2

So we get the following:

`f(x) = √(x^2-4)\\\\f(g(x)) = √((g(x))^2-4)\\\\f(g(x)) = √((3x-2)^2-4)\\\\f(g(x)) = √(9x^2-12x+4-4)\\\\f(g(x)) = √(9x^2-12x)\\\\`

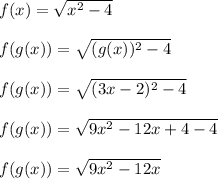
Next, we apply the derivative

`f(g(x)) = √(9x^2-12x)\\\\f(g(x)) = (9x^2-12x)^(1/2)\\\\f'(g(x)) = (1)/(2)(9x^2-12x)^(-1/2)*(d)/(dx)(9x^2-12x)\\\\f'(g(x)) = (1)/(2)(9x^2-12x)^(-1/2)*(18x-12)\\\\f'(g(x)) = (9x-6)/(√(9x^2-12x))\\\\`

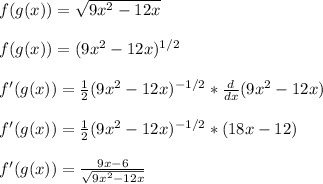
Don't forget about the chain rule. The chain rule is applied in step 3 of that block of steps shown above.

The last thing we do is plug in x = 3 and simplify.

`f'(g(x)) = (9x-6)/(√(9x^2-12x))\\\\f'(g(3)) = (9*3-6)/(√(9*3^2-12*3))\\\\f'(g(3)) = (21)/(√(45))\\\\f'(g(3)) = (21)/(√(9*5))\\\\f'(g(3)) = (21)/(√(9)*√(5))\\\\f'(g(3)) = (21)/(3*√(5))\\\\f'(g(3)) = (7)/(√(5))\\\\`

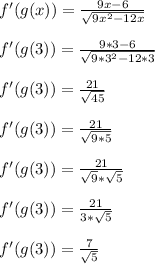
Side note: if you choose to rationalize the denominator, then you'll multiply both top and bottom by sqrt(5) to end up with
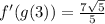`f'(g(3)) = (7√(5))/(5)\\\\`; however, your teacher has chosen not to rationalize the denominator.