Question

Question #5 Show steps
Correct answer is C

Answer 1

We need to find the derivative first. Think of x/(x+2) as x(x+2)^(-1). That will allow us to use the product rule. You could also use the quotient rule if you want. I'll go with the product rule route.

`f(x) = (x)/(x+2)\\\\f(x) = x(x+2)^(-1)\\\\f'(x) = (x+2)^(-1)-x(x+2)^(-2)\\\\f'(x) = (1)/(x+2)-(x)/((x+2)^2)\\\\f'(x) = (x+2)/((x+2)^2)-(x)/((x+2)^2)\\\\f'(x) = (x+2-x)/((x+2)^2)\\\\f'(x) = (2)/((x+2)^2)\\\\f'(x) = (2)/(x^2+4x+4)\\\\`

Since we want the tangent slope to be 1/2, we'll set f ' (x) equal to 1/2 and solve for x.

`f'(x) = (2)/(x^2+4x+4)\\\\(1)/(2) = (2)/(x^2+4x+4)\\\\1*(x^2+4x+4) = 2*2\\\\x^2+4x+4 = 4\\\\x^2+4x = 0\\\\x(x+4) = 0\\\\x = 0 \ \text{ or } \ x+4 = 0\\\\x = 0 \ \text{ or } \ x = -4\\\\`

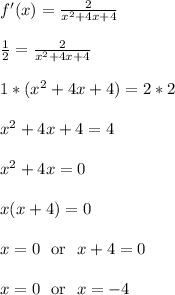
The two x values, x = 0 and x = -4, make f ' (x) equal to 1/2.

---------

If x = 0, then y is...

`y = f(x)\\\\f(x) = (x)/(x+2)\\\\f(0) = (0)/(0+2)\\\\f(0) = 0\\\\`

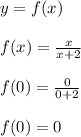
Showing that (0,0) is one point we're after.

If x = -4, then,

`y = f(x)\\\\f(x) = (x)/(x+2)\\\\f(-4) = (-4)/(-4+2)\\\\f(-4) = 2\\\\`

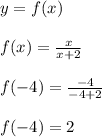
Making (-4, 2) the other point where the tangent slope is 1/2.

We use the original f(x) function, and not the derivative, when determining the y coordinates of the two points. If you plugged x = 0 or x = -4 into f ' (x), you'd get 1/2. So its good practice, but not what we're after ultimately.