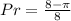Question

Q3 A dart is randomly thrown and lands within the boundaries of a 6 foot by 6 foot square. The unshaded regions are each a quarter of an inscribed circle. What is the probability that the dart lands in one of the shaded regions? Express your answer as a common fraction in terms of pi.​ PLEASE GIVE THE FULL EXPLANATION AND NOT JUST THE ANSWER!!!

Answer 1

`Pr = (8 - \pi)/(8)`

Explanation:

Given

See attachment for square

Required

Probability the
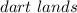`dart\ lands` on the shaded region

First, calculate the area of the square.

`Area = Length^2`

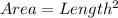
From the attachment, Length = 6;

So:

`A_1 = 6^2`

`A_1 = 36`

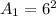
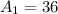
Next, calculate the area of the unshaded region.

From the attachment, 2 regions are unshaded. Each of this region is quadrant with equal radius.

When the two quadrants are merged together, they form a semi-circle.

So, the area of the unshaded region is the area of the semicircle.

This is calculated as:

`Area = (1)/(2) \pi d`

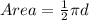
Where

`d = diameter`

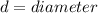
d = Length of the square

`d =6`

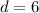
So, we have:

`Area = (1)/(2) \pi ((d)/(2))^2`

`Area = (1)/(2) \pi ((6)/(2))^2`

`Area = (1)/(2) \pi (3)^2`

`Area = (1)/(2) \pi *9`

`Area = \pi * 4.5`

`Area = 4.5\pi`

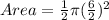
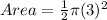
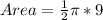
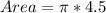
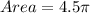
The area (A3) of the shaded region is:

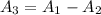`A_3 = A_1 - A_2` ---- Complement rule.

`A_3 = 36 - 4.5\pi`

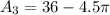
So, the probability that a dart lands on the shaded region is:

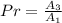`Pr = (A_3)/(A_1)` i.e. Area of shaded region divided by the area of the square

`Pr = (36 - 4.5\pi)/(36)`

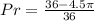
Factorize:

`Pr = (4.5(8 - \pi))/(36)`

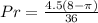
Simplify

`Pr = (8 - \pi)/(8)`