Question

A commuter crosses one of three bridges, A, B, or C, to go home from work. The commuter crosses bridge A with probability 1/3, crosses bridge B with probability 1/6, and crosses bridge C with probability 1/2. The commuter arrives home by 6pm with probability 75%, 60%, and 80% by crossing bridge A, B, or C, respectively. If the commuter arrives home by 6pm, find the probability that bridge B was used.

Answer 1

0.1333 = 13.33% probability that bridge B was used.

Explanation:

Conditional Probability

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

In which

P(B|A) is the probability of event B happening, given that A happened.

`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

In this question:

Event A: Arrives home by 6 pm

Event B: Bridge B used.

Probability of arriving home by 6 pm:

75% of 1/3(Bridge A)

60% of 1/6(Bridge B)

80% of 1/2(Bridge C)

So

`P(A) = 0.75*(1)/(3) + 0.6*(1)/(6) + 0.8*(1)/(2) = 0.75`

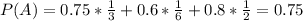
Probability of arriving home by 6 pm using Bridge B:

60% of 1/6. So

`P(A \cap B) = 0.6*(1)/(6) = 0.1`

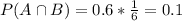
Find the probability that bridge B was used.

`P(B|A) = (P(A \cap B))/(P(A)) = (0.1)/(0.75) = 0.1333`

0.1333 = 13.33% probability that bridge B was used.