Final answer:
The length of the hypotenuse of the right triangle is approximately 9.22 feet.
Step-by-step explanation:
The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
In this case, the legs of the triangle are 6 feet and 7 feet long, respectively.
Using the Pythagorean theorem, we can calculate the length of the hypotenuse as follows:

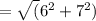
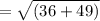
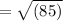
= 9.22 feet.