Question

The expression cube root of 54x^8y^12 can be written in simplest radical form as

Answer 1

The simplest radical form of the cubic root is
`3x^2y^4\sqrt[3]{2x}`

Explanation:

Cube root of 54x^8y^12

That is:

`\sqrt[3]{54x^8y^12}`

Can be simplified as:

`\sqrt[3]{54x^8y^12} = \sqrt[3]{54}\sqrt[3]{x^8}\sqrt[3]{y^12}`

We find each separate simplification, and multiply them:

Cubic root of 54:

`54 = 2*3^3`

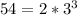
So

`\sqrt[3]{54} = \sqrt[3]{2*3^3} = 3\sqrt[3]{2}`

Cubic root of x^8

`\sqrt[3]{x^8} = \sqrt[3]{x^6*x^2} = x^2\sqrt[3]{x^2}`

Cubic root of y^12

`\sqrt[3]{y^(12)} = y^4`

Multiplying all these terms:

`\sqrt[3]{54}\sqrt[3]{x^8}\sqrt[3]{y^12} = 3\sqrt[3]{2}(x^2\sqrt[3]{x^2})(y^4) = 3x^2y^4\sqrt[3]{2x}`

The simplest radical form of the cubic root is
`3x^2y^4\sqrt[3]{2x}`