Answer:
Members of Team A are likely older, and they have less variability in their ages.
Explanation:
To solve this question, we need to find the mean and the standard deviation for each team.
Team A 16, 13, 12, 16, 13
The mean is:
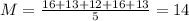
The standard deviation is:
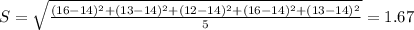
Team B: 10, 13, 16, 16, 10
The mean is:
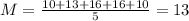
The standard deviation is:
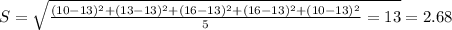
Which statement appropriately compares the ages of the team members?
Sample of team A has higher mean age, which means that they are likely older. They also have a smaller standard deviation, so they likely have less variability in their ages.