Question

Your local school board wants to determine the proportion of people who plan on voting for the school levy in the upcoming election. They conduct a random phone poll, where they contact 150 individuals and ask them whether or not they plan on voting for the levy. Of these 150 respondents, 78 people say they plan on voting for the levy. The school board wants to determine whether or not the data supports the idea that more than 50% of people plan on voting for the levy. Calculate the p-value for the one-sided Hypothesis test described in this example. (Hint: Find the test statistic and then use the tables to find the p-value.)

Answer 1

The p-value for the one-sided Hypothesis test described in this example is 0.3121.

Explanation:

Test the hypothesis that more than 50% of people plan on voting for the levy.

At the null hypothesis, we test that the proportion is 50%, that is:

`H_0: p = 0.5`

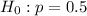
At the alternate hypothesis, we test if this proportion is above 50%, that is:

`H_a: p > 0.5`

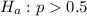
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`\sigma` is the standard deviation and n is the size of the sample.

0.5 is tested at the null hypothesis:

This means that
`\mu = 0.5, \sigma = √(0.5*0.5) = 0.5`

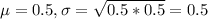
Of these 150 respondents, 78 people say they plan on voting for the levy.

This means that
`n = 150, X = (78)/(150) = 0.52`

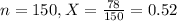
Value of the test statistic:

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (0.52 - 0.5)/((0.5)/(√(150)))`

`z = 0.49`

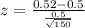
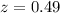
Pvalue of the test:

The pvalue of the test is the probability of finding a proportion above 0.52, which is 1 subtracted by the pvalue of z = 0.49.

Looking at the z-table, z = 0.49 has a pvalue of 0.6879.

1 - 0.6879 = 0.3121

The p-value for the one-sided Hypothesis test described in this example is 0.3121.