Answer:
Explanation:
1). Given equation is,
2x² - 3x = 6
2x² - 3x - 6 = 0
To find the solutions of the equation we will use quadratic formula,
x =

Substitute the values of a, b and c in the formula,
a = 2, b = -3 and c = -6
x =
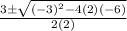
x =
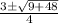
x =
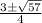
x =
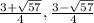
Therefore, there are two real solutions.
2). Given equation is,
x² + 1 = 2x
x² - 2x + 1 = 0
(x - 1)² = 0
x = 1
Therefore, there is one real solution of the equation.
3). 2x² + 3x + 2 = 0
By applying quadratic formula,
x =

x =
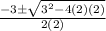
x =
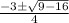
x =

x =
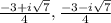
Therefore, there are two complex (non real) solutions.