Question

If ( 4x - 2 ) ( x + 9 ) - 3x = ax2 + bx + c, what is the value of b. The 2 is and exponent please help me 

Answer 1

b = -34

Explanation:

Use " ^ " to indicate exponentiation:

( 4x - 2 ) ( x + 9 ) - 3x = ax^2 + bx + c

Perform the indicated multiplication:

4x^2 + 36x - 2x - 18 - 3x becomes

4x^2 - 34x - 18 so b = -34

Answer 2

b=31 in
`ax^2+bx+c`

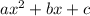
Explanation:

Hi there!

`( 4x - 2 ) ( x + 9 ) - 3x`

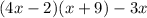
Our goal is to expand this equation and put it in the form
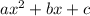`ax^2+bx+c`. Firstly, multiply the first two binomials (in the parentheses):

`= 4x(x+9)-2(x+9)-3x\\= 4x^2+36x-2(x+9)-3x\\= 4x^2+36x-2x-18-3x`

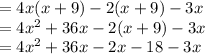
Now, we can combine like terms (terms with like variables):

`= 4x^2+36x-2x-3x-18\\= 4x^2+31x-18`

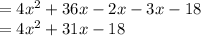
Now, in this equation, we can easily identify that 31 is the value of b in
`ax^2+bx+c`.

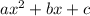I hope this helps!