Question

Find the area of the kite.

Answer 1

72

Explanation:

One way to do this is to use the formula
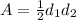`A=(1)/(2)d_1 d_2` where
`d_1` and
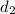`d_2` are the lengths of the two diagonals.

In the figure,
`d_1=12` and
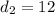`d_2=12` (2 + 10 and 6 + 6).

The area is
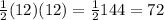`(1)/(2)(12)(12)=(1)/(2)144=72` square units.

Another way that doesn't depend on learning a formula is to remember that the diagonals of a kite are perpendicular, so the 4 small triangles are right triangles. Two of the smaller triangles have base =2 and height = 6, so their areas are 1/2(2)(6) = 6. Double that--there are 2 congruent small triangles--to get an area of 12.

There are two larger right triangles with base =10 and height = 6, so their area are 1/2(10)(6)=30. There are two of those, so their combined area is 60.

Finally, put the small triangle area and the large triangle area together to get a total of 12 + 60 = 72