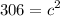Question

Cole found BC in ABC his work is shown below identify the first step in which his work shows an error

Can anyone help me with this question please.
No links or I’ll report.

Answer 1

The first step in Cole's work that shows an error is (C) Step 3:
`$306=c^2$`.

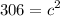In step 1, Cole correctly uses the Pythagorean theorem to express the relationship between the sides of the triangle.

In step 2, Cole correctly calculates the sum of the squares of the two shorter sides.

However, in step 3, Cole makes the mistake of equating the sum of the squares to the square of the hypotenuse. This is incorrect. The Pythagorean theorem states that the sum of the squares of the shorter sides is equal to the square of the hypotenuse, not the other way around.

Therefore, the correct equation should be:

`√(81+225)=c`

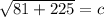
This will give the correct value for the length of the hypotenuse, BC.

Steps 4 and 5 are simply finding the square root of the correct expression and interpreting the result in the context of the problem. They are not the source of the error.

So, the answer is (C) Step 3:
`$306=c^2$`

Answer 2

Length of BC = 12 inch

Explanation:

Given:

ΔABC is a right angle triangle

Length of AB = 9 inch

Length of AC = 15 inch

Find;

Length of BC

Computation:

Using Pythagoreans theorem;

Hypotenues² = parpendicular² + Base²

Step 1 :

AC² = AB² + BC²

Step 2 :

15² = 9² + BC²

Step 3 :

225 = 81 + BC²

Step 4 :

225 - 81 = BC²

Step 5 :

BC² = 144

Step 6 :

BC = √144

Step 7 :

BC = 12 inch

Length of BC = 12 inch