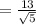Answer:
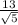
Explanation:
To get the shortest distance from a point to a line, we need to find a perpendicular line that intersects the line and also intersects the line. We know the slope of the line will be 1/2, but to find the y-intercept, we can just plug it into the point because we already know it will be on the line.
-3 = 1/2(-2)+c
-3 = -1+c
-2 = c
Now, we know the slope and the y-intercept, and since it will intersect the other line, we can set it equal to the other lines formula:
1/2x-2 = -2x+6
5/2x=8
x=16/5
Now, plugging this value of x into any of the equations, we can find the y-coordinate:
16/5(1/2)-2 = -2/5
We have the point (16/5, -2/5)
Now, we need to find the distance between (-2, -3) and (16/5, -2/5)
Plugging into distance formula:
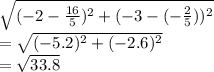
=