Question

At Sally's Hair Salon there are three hair stylists. 22% of the haircuts are done by Chris, 30% are done by Karine, and 48% are done by Amy. Chris finds that when he does haircuts, 5% of the customers are not satisfied. Karine finds that when she does haircuts, 3% of the customers are not satisfied. Amy finds that when she does haircuts, 7% of the customers are not satisfied. Suppose that a customer leaving the salon is selected at random. If the customer is not satisfied, what is the probability that their hair was done by Chris

Answer 1

0.2052 = 20.52% probability that their hair was done by Chris

Explanation:

Conditional Probability

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

In which

P(B|A) is the probability of event B happening, given that A happened.

`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

In this question:

Event A: Customer not satisfied

Event B: Hair done by Chris.

Probability of a customer not being satisfied.

5% of 22%(Chris)

3% of 30%(Karine)

7% of 48%(Amy)

This means that:

`P(A) = 0.05*0.22 + 0.03*0.3 + 0.07*0.48 = 0.0536`

Probaility of a customer not being satisfied and hair done by Chris:

5% of 22%. So

`P(A \cap B) = 0.05*0.22 = 0.011`

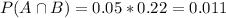
What is the probability that their hair was done by Chris?

`P(B|A) = (P(A \cap B))/(P(A)) = (0.011)/(0.0536) = 0.2052`

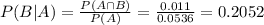
0.2052 = 20.52% probability that their hair was done by Chris