Question

An insurance company is obligated to pay a policyholder $500 in one year and $2,000 in 3 years. The insurance company has decided to employ the dedication strategy. The following assets are available: 1 year zero coupon bond with annual effective yield of 7%. 3 year zero coupon bond with annual effective yield of 8%. Determine the cost of establishing the asset portfolio.

Answer 1

The total cost of establishing the portfolio is $2054.95.

Step-by-step explanation:

The present value of a bond is given as

`PV=FV*(1)/((1+r)^n)`

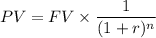
For 1 year zero-coupon bond is

• FV is 500
• r is 7% or 0.07
• n is 1

So the value is

`PV=FV*(1)/((1+r)^n)\\PV=500*(1)/((1+0.07)^1)\\PV=500*(1)/((1.07))\\PV=500*0.9346\\PV=\$ 467.29`

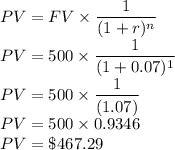
Similarly, for 3 years zero-coupon bond is

• FV is 2000
• r is 8% or 0.07
• n is 3

So the value is

`PV=FV*(1)/((1+r)^n)\\PV=2000*(1)/((1+0.08)^3)\\PV=2000*(1)/((1.08)^3)\\PV=2000*0.7938\\PV=\$ 1587.66`

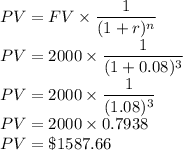
So the total cost is

Total Cost=Cost of 1-year zero-coupon bond+Cost of 3-years zero-coupon bond

Total Cost=$ 467.29+$ 1587.66

Total Cost= $ 2054.95

So the total cost of establishing the portfolio is $2054.95.