Question

A solid sphere, spherical shell, solid cylinder, and a cylindrical shell all have the same mass m and radius R. The same torque is applied on the rim for each of them, so that they all start to rotate about their long central axes from rest. Which object has the greatest angular speed after the same time interval

Answer 1

The solid sphere will have the greatest angular speed after the same torque is applied for the same time interval, because it has the smallest moment of inertia compared to a spherical shell, solid cylinder, and cylindrical shell with the same mass and radius.

Step-by-step explanation:

The question asks which object (a solid sphere, spherical shell, solid cylinder, or cylindrical shell) with the same mass m and radius R will have the greatest angular speed when the same torque is applied for the same time interval. To determine this, we need to understand how the moment of inertia impacts the angular acceleration, and hence the angular speed, of each object when subjected to the same torque.

The moment of inertia differs for each of the objects mentioned and plays a critical role in the dynamics of rotational motion. According to Newton's second law for rotation, the angular acceleration α is directly proportional to the applied torque τ and inversely proportional to the moment of inertia I, where α = τ / I. Thus, for the same applied torque, the object with the lowest moment of inertia will experience the highest angular acceleration and, consequently, reach the highest angular speed over the same time interval.

Among the given objects, the solid sphere has the smallest moment of inertia, given by Isphere = (2/5)mR², followed by the solid cylinder with Icylinder = (1/2)mR². The spherical shell and the cylindrical shell have greater moments of inertia because their masses are distributed further from the axis of rotation. The spherical shell has Ishell = (2/3)mR², and the cylindrical shell has the greatest moment of inertia of the four objects. Therefore, the solid sphere will achieve the greatest angular speed after the same torque is applied for the same time interval.

Answer 2

the solid sphere has the smallest moment thus angular veloicty is the largest in the system

Step-by-step explanation:

One of the easiest ways to solve this exercise is by using Newton's second law for rotational motion.

τ = I α

α = τ / I

now let's use the rotational kinematics relations

w = w₀ + α t

as the bodies start from rest, their angular velocity is zero w or = 0

w = α t

we substitute

w =
`(\tau )/(I) \ t`

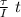
the body's inertia moments are

a) solid sphere I₁ = 2/5 m r²

b) spherical shell I₂ = ⅔ me r²

c) solid cylinder I₃ = ½ m r²

d) cylindrical shell I₄ = m r²

Let's analyze the expression for angular velocity, all bodies apply the same torque and it is measured in time, therefore the angular velocity is inversely proportional to the moment of inertia.

When examining the moment of inertia the largest is the moment of inertia of the cylindrical shell

the one with the lowest initial moment

we take all the values ​​to fractions with the same denominator

I₁ = 2/5 6/6 m r² = 12/30 m r²

I₂ = ⅔ 10/10 m r² = 20/30 m r²

I₃ = ½ 15/15 m r² = 15/30 m r²

therefore the order of the moments of inertia is

I₁ <I₃ <I₂ <I₄

Therefore, since the solid sphere has the smallest moment thus angular veloicty is the largest in the system