Answer:
The standard deviation of the sampling distribution of sample means would be of 0.6626 pounds.
Explanation:
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
 and standard deviation
and standard deviation
 , the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
 and standard deviation
and standard deviation
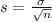 .
.
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
Standard deviation of 5.7 pounds.
This means that
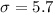
If a sampling distribution is created using samples of the amounts of weight lost by 74 people on this diet, what would be the standard deviation of the sampling distribution of sample means?
Sample of 74 means that
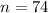
The standard deviaiton is:
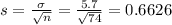
The standard deviation of the sampling distribution of sample means would be of 0.6626 pounds.