Question

The decay of 40K to 40Ar is used to date igneous rocks around fossil deposits to bracket the age of the fossils. When 40K decays, 10.9% of the time it produces 40Ar. The half-life of 40K is 1.248 x 109 years. In a given rock sample, 281.8 nmol of 40K is measured and 7.25 nmol of 40Ar is measured. What is the age of the rock in years

Answer 1

The age of the rock is 2.23x10⁹ years.

Step-by-step explanation:

The age of the rock can be calculated using the following equation:

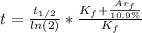`t = (t_(1/2))/(ln(2))*(K_(f) + (Ar_(f))/(10.9\%))/(K_(f))` (1)

Where:

t: is the age of the rock =?

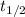`t_(1/2)`: is the half-life of ⁴⁰K = 1.248x10⁹ years

`K_(f)`: is the quantity of ⁴⁰K in the sample = 281.8x10⁻⁹ mol

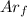`Ar_(f)`: is the quantity of ⁴⁰Ar in the sample = 7.25x10⁻⁹ mol

10.9%: is the percent of ⁴⁰Ar production by the decay of ⁴⁰K

By entering the above values into equation (1) we have:

`t = (1.248\cdot 10^(9) y)/(ln(2))*(281.8 \cdot 10^(-9) mol + (7.25 \cdot 10^(-9) mol)/(0.109))/(281.8 \cdot 10^(-9) mol)`

`t = 2.23 \cdot 10^(9) y`

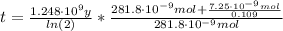
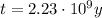
Therefore, the age of the rock is 2.23x10⁹ years.

I hope it helps you!