Answer:
95% of the confidence interval for q is
(0.05809 , 0.1183)
Explanation:
Step:1
Given that the random sample of 340 electronic components manufactured by a certain process is tested, and 30 are found to be defective.
sample proportion
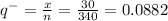
Step:2
95% of the confidence interval is determined by
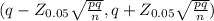
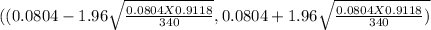
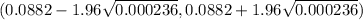
(0.0882 - 0.03011 , 0.0882+0.03011)
( 0.05809 , 0.1183)
Final answer:-
95% of the confidence interval for q is
(0.05809 , 0.1183)