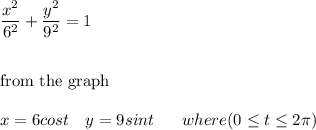Answer:
Explanation:
The description in terms of x and y when 0 ≤ t ≤ 2π can be computed as follows.
From the given information:
The major axis 2a = 18
a = 18/2
a = 9
i.e (0, ± 9)
On the minor axis; 2b = 12
b = 12/2
b = 6
(±6, 0)
The graph of the ellipse is displayed in the diagram below.
The description in term of x and y is: