Question

The 2003 Statistical Abstract of the United States reported that the percentage of people 18 years of age and older who smoke. Suppose that a study designed to collect new data on smokers and nonsmokers uses a preliminary estimate of the proportion who smoke of 0.30. a. [2.5 pts] How large a sample should be taken to estimate the proportion of smokers in the population with a margin of error of 0.02

Answer 1

A sample of 2017 should be taken.

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

In which

z is the zscore that has a pvalue of
`1 - (\alpha)/(2)`.

The margin of error is of:

`M = z\sqrt{(\pi(1-\pi))/(n)}`

Suppose that a study designed to collect new data on smokers and nonsmokers uses a preliminary estimate of the proportion who smoke of 0.30.

This means that
`\pi = 0.3`

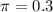
Confidence level:

Not given, so I will use 95%.

This means that
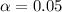`\alpha = 0.05`, z is the value of Z that has a pvalue of
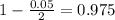`1 - (0.05)/(2) = 0.975`, so
`Z = 1.96`.

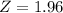a. [2.5 pts] How large a sample should be taken to estimate the proportion of smokers in the population with a margin of error of 0.02?

A sample of n should be taken.

n is found fo M = 0.02. So

`M = z\sqrt{(\pi(1-\pi))/(n)}`

`0.02 = 1.96\sqrt{(0.3*0.7)/(n)}`

`0.02√(n) = 1.96√(0.3*0.7)`

`√(n) = (1.96√(0.3*0.7))/(0.02)`

`(√(n))^2 = ((1.96√(0.3*0.7))/(0.02))^2`

`n = 2016.8`

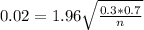
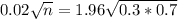
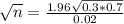
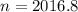
Rounding up:

A sample of 2017 should be taken.