Question

Babies born after 40 weeks gestation have a mean length of 52.2 centimeters (about 20.6 inches). Babies born one month early have a mean length of 47.4 cm. Assume both standard deviations are 2.5 cm. and the distributions are unimodal and symmetric. a. Find the standardized score (z-score), relative to all U.S. births, for a baby with a birth length of 45 cm. b. Find the standardized score of a birth length of 45 cm. for babies born one month early, using 47.4 as the mean. c. For which group is a birth length of 45 cm more common

Answer 1

a)
`Z = -2.88`

b)
`Z = -0.96`

c) 40 weeks gestation babies

Explanation:

Normal Probability Distribution:

Problems of normal distributions can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the z-score of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.

a. Find the standardized score (z-score), relative to all U.S. births, for a baby with a birth length of 45 cm.

Here, we use
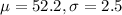`\mu = 52.2, \sigma = 2.5`. So

`Z = (X - \mu)/(\sigma)`

`Z = (45 - 52.2)/(2.5)`

`Z = -2.88`

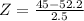
b. Find the standardized score of a birth length of 45 cm. for babies born one month early, using 47.4 as the mean.

Here, we use
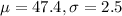`\mu = 47.4, \sigma = 2.5`. So

`Z = (X - \mu)/(\sigma)`

`Z = (45 - 47.4)/(2.5)`

`Z = -0.96`

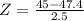
c. For which group is a birth length of 45 cm more common?

For each group, the probability is 1 subtracted by the pvalue of Z.

Z = -2.88 has a lower pvalue than Z = -0.96, so for Z = -2.88 the probability 1 - pvalue of Z will be greater. This means that for 40 weeks gestation babies a birth length of 45 cm is more common.