Answer:
The responses to these question can be defined as follows:
Explanation:

critical values
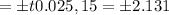
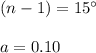
critical values

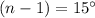
Testing the statistic values:
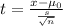
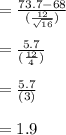
Test statistic ta
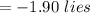
The critical values
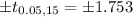
It is in the region of dismissal. We dismiss the 10% significant null hypothesis.

P - value is greater than the level of significance a= 0.05
Null hypothesis we don't reject. At a 95% level, the claim is justified.
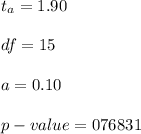
P - value below the meaning level a = 0.10, we reject the hypothesis null. At a level of 90% the claim is not justified.