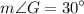Question

HELPPPP
please help me answer this question-

Answer 1

`\displaystyle GH = 2 √(30)`

`\displaystyle FH = 2 √(10)`

`\displaystyle m \angle G = {30}^( \circ)`

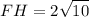
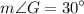
Explanation:

QUESTION-2:

we are given a right angle triangle

it's a 30-60-90 triangle of which FH is the shortest side

remember that,in case of 30-60-90 triangle the the longest side is twice as much as the shortest side thus

our equation is

`\displaystyle 2FH=4√(10)`

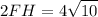
divide both sides by 2

`\displaystyle(2FH)/(2)= ( 4 √(10) )/(2)`

`\displaystyle FH =2 √(10)`

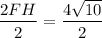
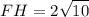
Question-1:

in order to figure out GH we can use Trigonometry because the given triangle is a right angle triangle

as we want to figure out GH we'll use sin function

remember that,

`\displaystyle \sin( \theta) = (opp)/(hypo)`

let our opp, hypo and
`\theta` be GH, 4√10 and 60° respectively

thus substitute:

`\displaystyle \sin( {60}^( \circ) ) = (GH)/(4 √(10) )`

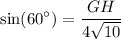
recall unit circle:

`\displaystyle ( √(3) )/(2) = (GH)/(4 √(10) )`

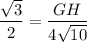
cross multiplication:

`\displaystyle 2 GH = 4 √(10) * √(3)`

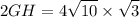
simplify multiplication:

`\displaystyle 2 GH = 4 √(30)`

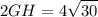
divide both sides by 2:

`\displaystyle GH = 2 √(30)`

QUESTION-3:

Recall that, the sum of the interior angles of a triangle is 180°

therefore,

`\displaystyle m \angle G + {60}^( \circ) + {90}^( \circ) = {180}^( \circ)`

simplify addition:

`\displaystyle m \angle G + {150}^( \circ) = {180}^( \circ)`

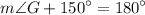
cancel 150° from both sides

`\displaystyle m \angle G = {30}^( \circ)`