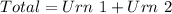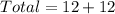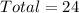Question

One urn contains one blue ball (labeled B1) and three red balls (labeled R1, R2, and R3). A second urn contains two red balls (R4 and R5) and two blue balls (B2 and B3). An experiment is performed in which one of the two urns is chosen at random and then two balls are randomly chosen from it, one after the other without replacement. a. Construct the possibility tree showing all possible outcomes of this experiment. b. What is the total number of outcomes of this experiment

Answer 1

(a) See attachment for tree diagram

(b) 24 possible outcomes

Explanation:

Given

`Urn\ 1 = \{B_1, R_1, R_2, R_3\}`

`Urn\ 2 = \{R_4, R_5, B_2, B_3\}`

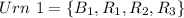
Solving (a): A possibility tree

If urn 1 is selected, the following selection exists:

`B_1 \to [R_1, R_2, R_3]; R_1 \to [B_1, R_2, R_3]; R_2 \to [B_1, R_1, R_3]; R_3 \to [B_1, R_1, R_2]`

If urn 2 is selected, the following selection exists:

`B_2 \to [B_3, R_4, R_5]; B_3 \to [B_2, R_4, R_5]; R_4 \to [B_2, B_3, R_5]; R_5 \to [B_2, B_3, R_4]`

See attachment for possibility tree

Solving (b): The total number of outcome

For urn 1

There are 4 balls in urn 1

`n = \{B_1,R_1,R_2,R_3\}`

Each of the balls has 3 subsets. i.e.

`B_1 \to [R_1, R_2, R_3]; R_1 \to [B_1, R_2, R_3]; R_2 \to [B_1, R_1, R_3]; R_3 \to [B_1, R_1, R_2]`

So, the selection is:

`Urn\ 1 = 4 * 3`

`Urn\ 1 = 12`

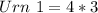
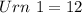
For urn 2

There are 4 balls in urn 2

`n = \{B_2,B_3,R_4,R_5\}`

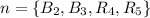
Each of the balls has 3 subsets. i.e.

`B_2 \to [B_3, R_4, R_5]; B_3 \to [B_2, R_4, R_5]; R_4 \to [B_2, B_3, R_5]; R_5 \to [B_2, B_3, R_4]`

So, the selection is:

`Urn\ 2 = 4 * 3`

`Urn\ 2 = 12`

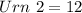
Total number of outcomes is:

`Total = Urn\ 1 + Urn\ 2`

`Total = 12 + 12`

`Total = 24`