Question

John invests a total of 10,000. He purchases an annuity with payments of 1,000 at the beginning of each year for 10 years at an effective annual interest rate of 8%. As annuity payments are received, they are reinvested at an effective annual interest rate of 7%. The remaining balance of the 10,000 is invested in a 10-year certificates of deposit with a nominal annual interest rate of 9%, compounded quarterly. Calculate the annual effective yield rate on the entire 10,000 investment over the 10-year period.

Answer 1

7.95%

Step-by-step explanation:

the first step is to determine the present value of the 10 year annuity

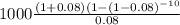`1000((1 + 0.08)(1 - (1 - 0.08)^(-10) )/(0.08)` = 7246.89

remaining balance of the 10,000 is invested in a 10-year certificates of deposit = 10,000 - 7246.89 = $2753.11

We would calculate the future value of this amount

The formula for calculating future value:

FV = P (1 + r/m)^mn

FV = Future value

P = Present value

R = interest rate

N = number of years

m = number of compounding

$2753.11 x ( 1 + 0.09/4)^(4 x 10) = 6704.34

calculate the value of reinvestments

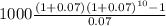`1000((1 + 0.07) ( 1 + 0.07)^(10) - 1 )/(0.07)` = 14783.60

14783.60 + 6704.34 = 10,000 ( 1 + er)^10

er = 0.0795 = 7.95%