Question

Given: triangle KLM, KL=LM, m

Answer 1

Approximately 1.2078566715...

Explanation:

Very tricky question! Because the picture doesn't seem to be drawn to scale...

With point O being the center of the circle, construct segments KO, LO, and MO, all of them are the radius of the circle, thus, equivalent.

Since KL=LM, then triangle KLM is an isosceles triangle and angle K is equal to angle M.

`m<K=m<M\\17=m<M`

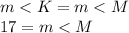
(Yes that means "measure of angle")

And because both angles K and M are 17 degrees, then angle L must be 146 degrees.

Now, focus on triangle LOK, since KO=LO, triangle LOK is also an isosceles triangle, thus:

`m<LKO=m<KLO\\m<LKO=73`

(Since half of angle L is 73)

Then m<KOL must be 34 degrees, and m<KOM will be 68 degrees.

After that, we can use the law of cosine to solve for KM:

`(KM)^2=1.08^2+1.08^2-2(1.08)(1.08)Cos(68)\\(KM)^2=1.1664+1.1664-2.3328(0.37460659341...)\\(KM)^2=2.3328-0.87388226112...\\(KM)^2=1.45891773888...\\KM=1.2078566715...`

The only thing that bothers me is angle KOM being 68 degrees because in the figure angle KOM is clearly an obtuse angle.

I hope I am not tripping.

Answer 2

Explanation:

Draw a really careful diagram of Circle with center O and ΔKLM Then make <K = 17° and <M = 17°

Draw line Segment LO

Draw line Segment KO

Mark the intersection point of LO and KM as C

Since KL = LM the vertex is

<KLM + 17 + 17 = 180

<KLM + 34 = 180

<KLM = 180 - 34

<KLM = 146

The diagonal LO bisects < KLM

Therefore <KL0 = 1/2 <KLM

<KLO = 73

KM and LO intersect at right angles because ΔKCL and MCL are congruent making <KCL = <MCL

2x = 180

x = 90

Now consider ΔKLO

It isosceles because it is made up of 2 radii.

That means that <OKL = 73

But OKC + OKL = 73

<OKC + 17 = 73

<OKC = 56

Now we are home free. We have the hypotenuse and an angle. We can find KC

Cos(56) = KC/KO

Cos(56) = KC/1.08

0.5592 * 1.08 = KC

kc = 0.6039

KM = twice that amount which is 1.2079