Question

Please help!! ABCD is a square. If AC = 26, Find BC

a. 7
b. 26
c. 12
d. 18.4

Answer 1

Since this is a square and we have the diagonal, we can use the formula Square root of 2 times d/2 where the diagonal is d, we can find the side (sqrt 2 * d/2)
sqrt 2 * 26/2 = 18.38. Rounding our decimal we get 18.4, so the answer is d. Hope this helps

Answer 2

Given :-

• the shape is a Square
• AC = 26.

`\\ \\`

To find:-

• BC

`\\ \\`

Solution:-

Let AC = x.

`\\`

As given figureis square, therefore all sides are equal :-

• AB = x
• AD = x
• DC = x

`\\`

So now instead of square focus on triangle ABC.

where :-

`\small \rm \angle B = 90 \degree`

`\\`

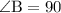
Equation formed:-

`\\ \\`

`\rm \dashrightarrow AC {}^(2) = AB {}^(2) + BC {}^(2)`

`\\`

`\rm \dashrightarrow 26 {}^(2) = x{}^(2) + x {}^(2)`

`\\`

`\rm \dashrightarrow 26 {}^(2) =2x {}^(2)`

`\\`

`\rm \dashrightarrow 26 * 26 =2x {}^(2)`

`\\`

`\rm \dashrightarrow2x {}^(2) = 26 * 26`

`\\ \\`

`\rm \dashrightarrow x {}^(2)=( 26 * 26 )/(2)`

`\\ \\`

`\rm \dashrightarrow x {}^(2)=\frac{ 26 * \cancel{26 }}{\cancel{2}}`

`\\ \\`

`\rm \dashrightarrow x {}^(2)=( 26 * 13)/(1)`

`\\ \\`

`\rm \dashrightarrow x {}^(2)=26 * 13`

`\\`

`\rm \dashrightarrow x = √(26 * 13)`

`\\`

`\rm \dashrightarrow x = √(338)`

`\\`

`\bf \dashrightarrow x = 18.38`

`\\ \\`

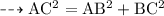
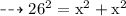
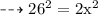
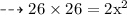
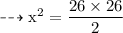
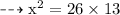
Formula used:-

`\bigstar \boxed{\tt Hypotenuse^2 = Base^2+Perpendicular^2}`

`\\ \\`

Therefore BC is equal to 18.38 cm.

____________________

⭑Related Concept⭑

Property of square:-

• All sides of square are equal.

• All angles of square are equal.

• All angles of square are in 90°.

• The diagonals of a square bisect each other and meet at 90°.

• There are four sides and four angles in square.

• Opposite sides of a square are parallel to each other.