Question

According to a study in a medical journal, 202 of a sample of 5,990 middle-aged men had developed diabetes. It also found that men who were very active (burning about 3,500 calories daily) were a fourth as likely to develop diabetes compared with men who were sedentary. Assume that one-fifth of all middle-aged men are very active, and the rest are classified as sedentary. What is the probability that a middle-aged man with diabetes is very active

Answer 1

0.0588 = 5.88% probability that a middle-aged man with diabetes is very active

Explanation:

Conditional Probability

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

In which

P(B|A) is the probability of event B happening, given that A happened.

`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

In this question:

Event A: Has diabetes.

Event B: Is very active.

Probability of having diabetes:

To find this probability, we take in consideration that:

It also found that men who were very active (burning about 3,500 calories daily) were a fourth as likely to develop diabetes compared with men who were sedentary. Assume that one-fifth of all middle-aged men are very active, and the rest are classified as sedentary.

So the probability of developing diabetes is:

x of 4/5 = x of 0.8(not active)

x/4 = 0.25x of 1/5 = 0.2(very active). So

`P(A) = 0.8x + 0.25*0.2x = 0.85x`

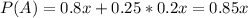
Probability of developing diabetes while being very active:

0.25x of 0.2. So

`P(A \cap B) = 0.25x*0.2 = 0.05x`

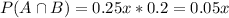
What is the probability that a middle-aged man with diabetes is very active?

`P(B|A) = (P(A \cap B))/(P(A)) = (0.05x)/(0.85x) = (0.05)/(0.85) = 0.0588`

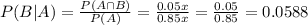
0.0588 = 5.88% probability that a middle-aged man with diabetes is very active