Question

Please math , help

You are given the results of measurement of resistors. We are testing the
measurement tool. It will pass the technical control if the mean value will be
in the range [198-202] with standard deviation less than 3 Ohms. Will the tool
pass the technical control?

Answer 1

As both the mean and standard deviation are in the desired ranges, the tool passes the technical control.

Explanation:

Mean of the batch:

The mean of the batch is the sum of all values divided by the number of items. So

`M = (199+204+201+197+195+204+200)/(7) = 200`

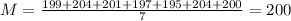
Mean in the desired interval.

Standard deviation:

Square root of the sum of the difference squared between each term and the mean, divided by the number of items. So

`S = \sqrt{((199-200)^2+(204-200)^2+(201-200)^2+(197-200)^2+(195-200)^2+(204-200)^2+(200-200)^2)/(7)} = 1.18`

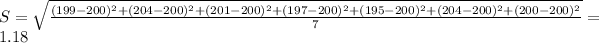
As both the mean and standard deviation are in the desired ranges, the tool passes the technical control.