Question

Can someone please help me with this logarithm equation!!

Answer 1

`(629)/(2)`

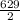
Explanation:

So, our equation is:

`log_5((2x-4)/(5)) = 3`

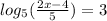
In exponetial form, this looks like:

`5^3=(2x-4)/(5)`

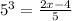
Now lets cube the 5:

`125=(2x-4)/(5)`

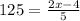
Next, we can multiply the denominator on the right side by 5:

`625=2x-4`

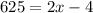
We need to now get x alone by adding 4 to both sides:

`629=2x`

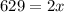
Finally, we divide by x's coefficent, 2, to get:

`x=(629)/(2)`

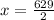
Hope this helps! :3