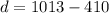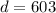Question

The table of values represents a function ​f(x).

How much greater is the average rate of change over the interval [7, 9] than the interval [4, 6]?



Enter your answer in the box.

Answer 1

603

Explanation:

i took it

Answer 2

It is 603 units greater

Explanation:

Given

See attachment for table

Average rate of change over (a,b) is calculated as:

`Rate = (f(b) - f(a))/(b-a)`

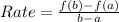
For interval [7,9], we have:

`[a,b] = [7,9]`

So, we have:

`Rate = (f(9) - f(7))/(9-7)`

`Rate = (f(9) - f(7))/(2)`

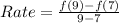
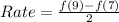
From the table:

`f(9) = 3878`

`f(7) = 1852`

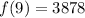
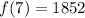
So:

`Rate = (f(9) - f(7))/(2)`

`Rate = (3878 - 1852)/(2)`

`Rate = (2026)/(2)`

`Rate = 1013\\`

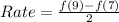
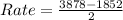
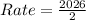
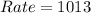
For interval [4,6], we have:

`[a,b] = [4,6]`

So, we have:

`Rate = (f(6) - f(4))/(6-4)`

`Rate = (f(6) - f(4))/(2)`

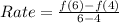
From the table:

`f(6) = 1178`

`f(4) = 358`

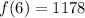
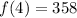
So:

`Rate = (f(6) - f(4))/(2)`

`Rate = (1178 - 358)/(2)`

`Rate = (820)/(2)`

`Rate = 410`

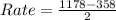
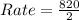
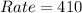
Calculate the difference (d) to get how much greater their rate of change is:

`d = 1013 - 410`

`d = 603`