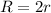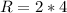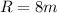Answer:
 --- small circle
--- small circle
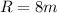 --- big circle
--- big circle
Explanation:
Given
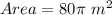 -- sum of areas
-- sum of areas
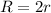
Required
The radius of the larger circle
Area is calculated as;
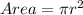
For the smaller circle, we have:
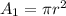
For the big, we have
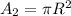
The sum of both is:

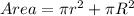
Substitute:
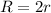
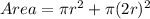
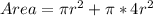
Substitute
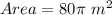
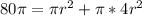
Factorize
![80\pi = \pi[ r^2 + 4r^2]](https://img.qammunity.org/2022/formulas/mathematics/college/5r02d2pfl7bdkatwyv9bw5a7ath9bcwsxc.png)
![80\pi = \pi[ 5r^2]](https://img.qammunity.org/2022/formulas/mathematics/college/5d66ausz1zc92az42w6gtaaemhgkg2s85p.png)
Divide both sides by

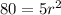
Divide both sides by 5
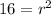
Take square roots of both sides
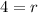

The radius of the larger circle is: