Answer:
Electric force is 1.23 x 10³⁶ times stronger than gravitational force.
Step-by-step explanation:
First, we will calculate the gravitational force using Newton's Law:
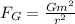
where,
F_G = Gravitational Force = ?
G = Gravitational Constant = 6.67 x 10⁻¹¹ Nm²/kg²
m = mass of proton = 1.67 x 10⁻²⁷ kg
r = distance between protons
Therefore,
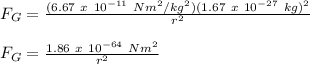
Now, we will calculate the electrostatic force using Colomb's Law:
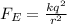
where,
F_E = Electrostatic Force = ?
k = Colomb's Constant = 9 x 10⁹ Nm²/C²
q = charge of proton = 1.6 x 10⁻¹⁹ C
r = distance between protons
Therefore,
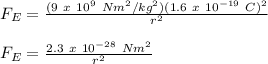
Dividing both forces:
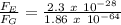
F_E = 1.23 x 10³⁶ F_G
Therefore, electric force is 1.23 x 10³⁶ times stronger than gravitational force.