Question

What is the value of the expression below? (64^3)^1/6

Answer 1

8

Explanation:

Remember the phrase "power to a power means to multiply the exponents"

That is, if you have a number (call it x) raised to a power (call it b), and that whole expression is raised to a power (call it c), it's the same as that number x raised to the power of the product of those two powers.

`(x^a)^b = x^a^b`

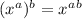
Here's an example showing to give some intuition behind this (and a way to derive the above formula if you forget it):

`x^3 = x*x*x\\(x^3)^2 = (x*x*x)^2 = x*x*x*x*x*x = x^6`

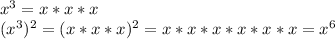
Or more simply,

`(x^3)^2 = x^(^3^*^2^) = x^6`

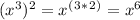
So in this case:

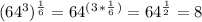`(64^3)^(1)/(6) = 64^(^3^*^(1)/(6)^) = 64^(1)/(2) = 8` (remember a number raised the to the power of 1/2 is the square root of the number; in this case, the square root of 64 is 8)

Answer 2

(64^3)^(1/6)

=(64)^(3×1/6)

=(64)^(1/2)

=(8^2)^(1/2)

=(8)^(2×1/2)

=8^1

=8

8 is the correct answer of your question...