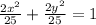Question

A space probe flies by a planet in an hyperbolic orbit. It reaches the vertex of its orbit at (5,0) and then travels along a 2 path that gets closer and closer to the line y=-x. Write an equation that describes the path of the space probe if the 5 center of its hyperbolic orbit is at (0,0).​

Answer 1

`\frac{2x^(2) }{{25} } + \frac{2y^(2)}{{25} } = 1`

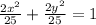
Explanation:

Since the required hyperbola has its vertex at (5,0), its transverse axis is on the x-axis and center at (0,0).

So, we use the equation in standard form

`(x^(2) )/(a^(2) ) + (y^(2) )/(b^(2) ) = 1`

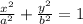
Also, since the path of the space probe gets closer to y = -x, this is the asymptote to the hyperbola.

Our standard asymptote equation is y = ±bx/a taking the negative sign and comparing with y = -x,

-bx/a = -x ⇒ b/a = 1 ⇒ a = b

Also, the coordinate of the vertex (c, 0) = (5, 0) and c² = a² + b²

substituting c = 5 and a = b into the equation, we have

c² = a² + b²

5² = a² + a²

25 = 2a²

a² = 25/2

a = √(25/2)

a = ±5/√2

rationalizing, we have

a = ±5/√2 × √2/√2

a = ±5√2/2

Since a = b, b = ±5√2/2

Inserting a and b into the equation for the hyperbola, we have

`(x^(2) )/(a^(2) ) + (y^(2) )/(b^(2) ) = 1\\(x^(2) )/(((5√(2) )/(2) )^(2) ) + (y^(2) )/((5√(2) )/(2) ^(2) ) = 1\\(x^(2) )/((25 X 2 )/(4) ) + (y^(2) )/((25X2 )/(4) ) = 1\\(x^(2) )/((25)/(2) ) + (y^(2) )/((25)/(2) ) = 1\\\frac{2x^(2) }{{25} } + \frac{2y^(2)}{{25} } = 1`

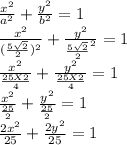
So, the required equation is

`\frac{2x^(2) }{{25} } + \frac{2y^(2)}{{25} } = 1`