Answer:
Approximately
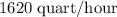 .
.
Explanation:
The given quantity was in the unit
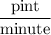 while the required quantity should have the unit
while the required quantity should have the unit
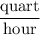 . It would thus be necessary to use conversion factors of the following forms:
. It would thus be necessary to use conversion factors of the following forms:
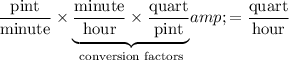 .
.
Make use of the fact that:
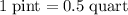 , and
, and
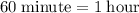 .
.
Rearrange the equation
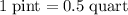 to obtain the conversion factor:
to obtain the conversion factor:
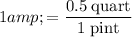 .
.
Similarly, rearrange the equation
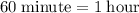 to obtain the conversion factor:
to obtain the conversion factor:
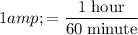 .
.
Combine both conversion factors and evaluate:
 .
.