Question

Find the area of the shade region.round to the nearest tenth

Answer 1

450.5 in²

Explanation:

The area of the triangle

= (20×21)/2

= 210 in²

The hypotenuse of the triangle

=
`\sqrt{ {20}^(2) + {21}^(2) }`

=
`√(400 + 441)`

=
`√(841)`

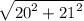
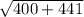
= 29 in

The hypotenuse of the triangle (29 in)

= the diameter of the circle

The formula of area of a circle= πr²

The radius of the circle

= 29÷2

= 14.5 in

The area of the circle

= π × 14.5²

= 660.5 in² (rounded to the nearest tenth)

The area of the shaded region

= 660.5 - 210

= 450.5 in²

Answer 2

189.25

Explanation:

first you find the area of the entire circle which is π times (14.5) squared so 210.25π. then you find the triangle which is 1/2 20×21= 21 then subtract 210.25π by 21= 189.25