Question

While performing a stunt, Danger Dog rides his motorcycle off the edge of a cliff with a velocity of 32 m/s. If the cliff is 45 m high, how far from the base of the cliff will Danger Dog land? Enter your answer in meters. 11 m 96 m 288 m 4 m

Answer 1

The correct answer is b: 96 m.

Step-by-step explanation:

The total distance in the horizontal direction traveled by Danger Dog can be calculated using the following equation:

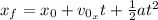`x_(f) = x_(0) + v_{0_(x)}t + (1)/(2)at^(2)` (1)

Where:

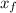`x_(f)`: is the final position in the horizontal direction =?

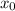`x_(0)`: is the initial position in the horizontal direction = 0

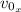`v_{0_(x)}`: is the initial velocity in the horizontal direction = 32 m/s

t: is the time

a: is the acceleration = 0 (he is accelerated only by gravity)

So, we need to find the time. We can find it as follows:

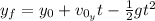`y_(f) = y_(0) + v_{0_(y)}t - (1)/(2)gt^(2)` (2)

Where:

`y_(f)`: is the final position in the vertical direction = 0

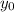`y_(0)`: is the initial position in the vertical direction = 45 m

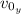`v_{0_(y)}`: is the initial velocity in the vertical direction = 0

g: is the acceleration due to gravity = 10 m/s²

By solving equation (2) for "t" we have:

`t = \sqrt{(2(y_(0) - y_(f)))/(g)} = \sqrt{(2*45 m)/(10 m/s^(2))} = 3 s`

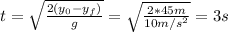
Hence, the total distance traveled by Danger Dog in the x-direction is (equation 1):

`x_(f) = 32 m/s*3 s = 96 m`

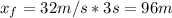
Therefore, the correct answer is b: 96 m.

I hope it helps you!