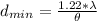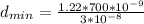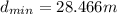Question

The lens of a telescope has a diameter of 25 cm. You are using it to look at two stars that are 2 × 1017 m away from you and 6 × 109 m from each other. You are measuring light with a wavelength of 700 nm. As the light goes through the lens, it diffracts. a. Is it possible, using this telescope, to see the two stars as separate stars? b. What is the minimum possible lens diameter you would need in order to resolve these two stars?

Answer 1

a)It is NOT possible using this telescope, to see the two stars as separate stars

b)
`d_(min) =28.466m`

Step-by-step explanation:

From the question we are told that:

Diameter of lens,
`d = 25 cm \approx 0.25 m`

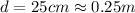
Distance from both star
`D_f= 2*10^(17) m`

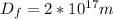
Distance between both stars
`D_b= 6*10^9 m`

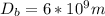
Wavelength of light
`\lambda =700 nm \approx 700*10^-9 m`

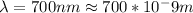
Generally the equation for angle subtended by the two stars at the lens is mathematically given by

`\theta=(D_f)/(D_b)`

`\theta=(6*10^9)/(2*10^(17))`

`\theta=3.0*10^(-8) rad`

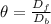
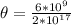
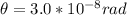
Generally the equation for minimum angular separation of two object is mathematically given by

`\theta_(min) = 1.22*\lambda/d`

`\theta_(min)= (1.22*700*10^-9)/(0.25)`

`\theta_(min)= 3.416*10^-^6 rad`

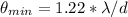
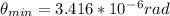
Therefore

`\theta < \theta_(min)`

`3.0*10^(-8) rad< 3.416*10^-^6 rad`

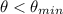
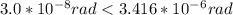
It is NOT possible using this telescope, to see the two stars as separate stars

b)

Generally the equation for minimum diameter of the lens is mathematically given by

`d_(min) =( 1.22*\lambda)/(\theta)`

`d_(min) =( 1.22*700*10^(-9))/(3*10^(-8))`

`d_(min) =28.466m`