Question

Fig. A shows a paper cup in the shape of an inverted right circular cone. Its base radius is 4 cm and its slant height is 8.5 cm.

(a) Find the capacity of the paper cup.

(b) The paper cup is cut along PQ to form the sector in Fig. B. Find
(i) the area of the sector,
(ii) the angle of the sector.

(a)
Height of the cup
=
`\sqrt{ {8.5}^(2) - {4}^(2) }`
= 7.5 cm
The capacity of the cup
=
`(1)/(3) * \pi * {4}^(2) * 7.5`
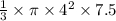
= 126 cm³ (cor. to 3 sig. fig.)

(b)(i)
The area of the sector
=
`\pi * 4 * 8.5`
= 107 cm² (cor. to 3 sig. fig.)

Can you help me for (b)(ii)?​

Answer 1

169° (3sf)

Explanation:

the area of a circle multiplied by the angle over 360 gives you ans.

x/360 × π × r²=34π -> ur ans frm part i

x × π(8.5²)=12240π

x × 72.25=12240

x=169.41°

Answer 2

9514 1404 393

Answer:

16π/17 radians ≈ 169.41°

Explanation:

The arc length of the sector is the circumference of the cone:

C = 2πr = 2π(4 cm) = 8π cm

The angle and arc length are related by ...

s = rθ . . . . . θ in radians

8π cm = (8.5 cm)θ

θ = 8π/8.5 = 16π/17 . . . . radians

bii) The angle of the sector is 16π/17 radians ≈ 169.41°.