Answer:
a) T = 1.69 s, b) k = 0.825 N / m, c) v = 1.46 feet/s, d) a = 5.41 ft / s²,
e) v = - 1,319 ft / s, a = - 2.70 ft / s², f) K = 4.8 10⁻³ J, U = 1.49 10⁻³ J
Step-by-step explanation:
In a mass-spring system with simple harmonic motion, the angular velocity is
w =
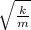
a) find the period
angular velocity, frequency, and period are related
w = 2π f = 2π / T
f = 1 / T
T = 1 / f
T = 1 / 0.59
T = 1.69 s
b) the spring constant
w = 2π f
w = 2π 0.59
w = 3.70 rad / s
w² = k / m
k = w² m
k = 3.70² 0.060
k = 0.825 N / m
c) the maximum speed
simple harmonic movement is described by the expression
x = A cos (wt + Ф)
speed is defined by
v =

v = -A w sin (wt + fi)
the speed is maximum when the cosine is ± 1
v = A w
v = 0.394 3.70
v = 1.46 feet/s
d) maximum acceleration
a =
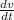
a = - A w² cos wt + fi
the acceleration is maximum when the cosine is ±1
a = A w²
a = 0.394 3.70²
a = 5.41 ft / s²
e) velocity and acceleration for x = 6 cm
let's reduce the cm to feet
x = 6 cm (1 foot / 30.48 cm) = 0.1969 foot
Before doing this part we must find the phase angle (Ф), the most common way to start the movement is to move the spring a small distance and release it, so its initial speed is zero for t = 0 s
let's use the expression for the velocity
v = -A w sin (0 + Фi)
0 = - A w sin Ф
so sin Ф = 0 which implies that Фi = 0
the equation of motion is
x = A cos wt
x = 0.394 cos 3.70t
we substitute
0.1969 = 0.394 cos 370t
3.70 t = cos⁻¹ (0.1969 / 0.394)
let's not forget that the angle is in radians
3.70, t = 1.047
t = 1.047 / 3.70
t = 0.2826 s
we substitute this time in the equation for velocity and acceleration
v = - Aw sin wt
v = - 0.394 3.70 sin 3.70 0.2826
v = - 1,319 ft / s
a = - A w² cos wt
a = - 0.394 3.70² cos 3.70 0.2826
a = - 2.70 ft / s²
f) the kinetic and potential energy at this point
K = ½ m v²
let's slow down to the SI system
v = 1.319 ft / s (1 m / 3.28 ft) = 0.402 m / s
K = ½ 0.060 0.402²
K = 4.8 10⁻³ J
U = ½ k x²
U = ½ 0.825 0.06²
U = 1.49 10⁻³ J