Question

Use limits to find the area between the curve of y = x and the x-axis for the interval from

x= 1 to x= 3.
Links will be reported.

Answer 1

The area between the curves is 4 square units.

Explanation:

We want to find the area bounded by:

y = x

x = 0

in the interval x = 1, x = 3

This is simply equal to the integral of the function f(x) = x between x = 1 and x = 3

Written as:

`\int\limits^3_1 {x} \, dx`

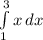
And the integral of x is equal to x^2/2

Then:

`\int\limits^3_1 {x} \, dx = ((3^2)/(2) - (1^2)/(2)) = ((9)/(2) - (1)/(2) ) = (8)/(2) = 4`

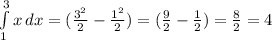
The area between the curves is 4 square units.