Question

This a solving question

Please please help

Answer 1

Part A

The sound intensity at the location 150 from the firework = 4.3
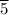`\overline 5` W/m²

Part B

The power the firework is emitting is approximately 1,231.5 kW

Step-by-step explanation:

Part A

The data of the firework sound heard by the two friends are;

Let 'A' represent the location of the friend at a point 150 m from the fireworks and let 'B' represent the location of the friend watching from a distance of 700 m from the firework

The distance of 'A' from the sound, r₁ = 150 m

The distance of 'B' from the sound, r₂ = 700 m

The intensity at which 'B' hears the sound, I₂ = 0.2 W/m²

The relationship between sound intensity and distance is given as follows;

`(I_2)/(I_1) = \left ((r_1)/(r_2) \right )^2`

`\therefore {I_1} = (I_2)/( \left ((r_1)/(r_2) \right )^2) = I_2 * \left ((r_2)/(r_1) \right )^2`

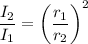
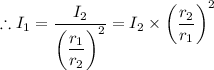
Plugging in the values gives;

`\therefore {I_1} = 0.2 * \left ((700)/(150) \right )^2 = (196)/(45) = 4.3\overline 5`

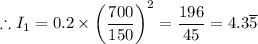
The sound intensity at location 'A', I₁ = 4.3
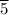`\overline 5` W/m²

Part B

The relationship between power, 'P', and intensity, 'I', is presented as follows;

`I = (P)/(4 \cdot \pi \cdot r^2)`

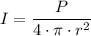
P = I·4·π·r² = 4·I·π·r²

Therefore, at point 'A', where the distance, r₁ = 150 m, and the intensity, I₁ = 4.3
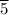`\overline 5` W/m², we have;

P = 4 × 4.3
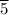`\overline 5` W/m² × π × (150 m)² = 1231504.32021 W

The power the firework is emitting, P ≈ 1,231.5 kW.