Question

A study published in Psychiatry Research states that 62% of autistic children are left-handed.[12]

A local resource for children with autism, Central Coast Autism Learning Partners, is curious to see
if their set of autistic children show a similar proportion of being left-handed. When a random
sample of 26 autistic children were observed, 17 were found to be left-handed. Is there enough
statistical evidence based on the sample to dispute the results of the study published in Psychiatry
Research? Use the P-value method and let
a=.05.

Answer 1

The pvalue of the test is 0.7188 > 0.05, which means that there is not enough statistical evidence based on the sample to dispute the results of the study published in Psychiatry Research.

Explanation:

Test if there is enough statistical evidence based on the sample to dispute the results of the study published in Psychiatry Research:

This means that at the null hypothesis we test if the proportion is 62%, that is:

`H_0: p = 0.62`

At the alternate hypothesis, we test if the proportion is different from 0.62, that is:

`H_a: p \\eq 0.62`

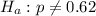
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`\sigma` is the standard deviation and n is the size of the sample

62% is tested at the null hypothesis:

This means that
`\mu = 0.62, \sigma = √(0.62*0.38)`

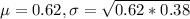
When a random sample of 26 autistic children were observed, 17 were found to be left-handed.

This means that
`n = 26, X = (17)/(26) = 0.6538`

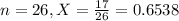
Value of the test statistic:

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (0.6538 - 0.62)/((√(0.62*0.38))/(√(26)))`

`z = 0.36`

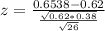
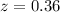
Pvalue of test and decision:

The pvalue of the test is the probability of a proportion that differs from the mean by at least 0.6538 - 0.62 = 0.0338, which is P(|z| > 0.36), which is two multiplied by the pvalue of z = -0.36

Looking at the z-table, z = -0.36 has a pvalue of 0.3594

2*0.3594 = 0.7188

The pvalue of the test is 0.7188 > 0.05, which means that there is not enough statistical evidence based on the sample to dispute the results of the study published in Psychiatry Research.