Find the f^-1(x) and it’s domain

Question

asked Aug 24, 2022 102k views

1 Answer

Pere · Answer 1 · 2022-08-30T17:54:27+0000

Answer:

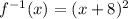
f^(-1)(x) = (x + 8)^2

$x \ge -8$

Explanation:

Given

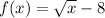
$f(x) = \sqrt x - 8$

Solving (a):
f^(-1)(x)

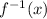
We have:

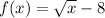
$f(x) = \sqrt x - 8$

Express f(x) as y

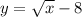
$y = \sqrt x - 8$

Swap x and y

$x = \sqrt y - 8$

Add 8 to
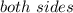
$both\ sides$

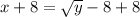
$x + 8 = \sqrt y - 8 + 8$

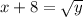
$x + 8 = \sqrt y$

Square both sides

(x + 8)^2 = y

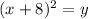
Rewrite as:

y = (x + 8)^2

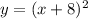
Express y as:
f^(-1)(x)

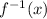
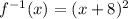
f^(-1)(x) = (x + 8)^2

To determine the domain, we have:

The original function is
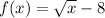
$f(x) = \sqrt x - 8$

The range of this is:
$f(x) \ge -8$

The
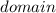domain of the
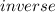inverse function is the
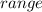range of the
original function.

Hence, the domain is:

$x \ge -8$