Question

A rollercoaster cart that has a mass of 4500 kg has 67.5 kJ (kilojoules), or 67,500 J (joules), of gravitational potential

energy. What is its height above the ground?
PT.2
The same 4500 kg rollercoaster cart is moving with 63.0 kJ (kilojoules), or 63,000 J (joules), of kinetic energy at the
bottom of its biggest hill. What is its velocity?

Answer 1

Answer: The height of rollercoaster cart above the ground is 1.53 m.

The velocity of rollercoaster cart is 5.29 m/s.

Step-by-step explanation:

Potential energy is the energy occupied by a substance due to its position. Formula for potential energy is as follows.

P.E = mgh

where,

m = mass of substance

g = gravitational constant =
`9.8 m/s^(2)`

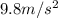
h = height

Substitute the values into above formula as follows.

`P.E = m * g * h\\67500 J = 4500 kg * 9.8 m/s^(2) * h\\h = (67500 J)/(4500 kg * 9.8 m/s^(2))\\= 1.53 m`

Hence, the height of rollercoaster cart above the ground is 1.53 m.

Kinetic energy is the energy occupied by the motion of a substance. Formula for kinetic energy is as follows.

`K.E = (1)/(2)m * v^(2)`

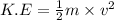
where,

m = mass of substance

v = velocity of substance

Substitute the values into above formula as follows.

`K.E = (1)/(2)m * v^(2)\\63000 J = (1)/(2) * 4500 kg * v^(2)\\v^(2) = (63000 J * 2)/(4500 kg)\\v = 5.29 m/s`

Hence, the velocity of rollercoaster cart is 5.29 m/s.