Answer:
A = 36.8°
B = 23.2°
a = 7.6
Explanation:
Given:
C = 120°
b = 5
c = 11
Required:
Find A, B, and a.
Solution:
✔️To find B, apply the Law of Sines
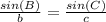
Plug in the values
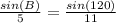
Cross multiply
Sin(B)*11 = sin(120)*5
Divide both sides by 11
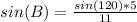
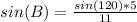
Sin(B) = 0.3936
B =
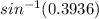
B = 23.1786882° ≈ 23.2° (nearest tenth)
✔️Find A:
A = 180° - (B + C) (sum of triangle)
A = 180° - (23.2° + 120°)
A = 36.8°
✔️To find a, apply the Law of sines:
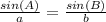
Plug in the values
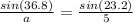
Cross multiply
a*sin(23.2) = 5*sin(36.8)
Divide both sides by sin(23.2)
![a = \frac{5*sin(36.8)}{sin(23.2)]()
a = 7.60294329 ≈ 7.6 (nearest tenth)