Question

In the accompanying diagram of circle O, chords AB and CD intersect at E and

AC:CB:BD:DÀ= 4:2:6:8
What is the measure of AC, BD, and DEB?

Answer 1

m(arc AC) = 72°

m(arc BD) = 108°

m∠DEB = 90°

Explanation:

Ratio of the measure of arc AC, arc BC, arc BD and arc AD = 4 : 2 : 6 : 8

Since, m(arc AC) + m(arc CB) + m(arc BD) + m(arc AD) = 360°

By the property of ratio,

Measure of arc AC =
`(4)/(4+2+6+8)* (360^0)`

=
`(4* 360)/(20)`

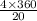
= 72°

Measure of arc BD =
`(6)/(4+2+6+8)* (360^0)`

=
`(6* 360)/(20)`

= 108°

Measure of ∠DEB =
`(1)/(2)m(arcAC + arc BD)`

=
`(1)/(2)(72+108)`

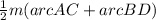
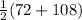
= 90°